Todas las organizaciones necesitan tomar decisiones. Con buenos datos, y con el empleo de modelos adecuados, estas decisiones serán las mejores posibles e incluso, bajo ciertas condiciones, serán óptimas.
En el ámbito de la logística y de la distribución, uno de los problemas clásicos es la determinación de la ruta óptima de un vehículo que ha de recorrer una serie de localizaciones. Se trata del conocido como Problema del Viajante o TSP, acrónimo con origen en la denominación de este problema en lengua inglesa: Traveling Salesman Problem.
El Problema del Viajante (TSP)
Aunque es algo difícil de demostrar de forma rigurosa, se puede decir que el TSP es el problema de optimización combinatoria más estudiado a lo largo de la historia. El enunciado del problema, en su forma más básica, es simple: Determinar la ruta más corta que permite a un viajante recorrer todas las ciudades de una determinada área geográfica, pasando por cada una de ellas una y sólo una vez, para, a continuación, volver al punto de inicio de la ruta.
Origen del TSP
Se puede decir que las raices del TSP son algo oscuras. Así, en 1.954, Dantzig, Fulkerson y Johnson, en su artículo «Solution of a large scale traveling Salesman problem» mencionan lo siguiente: «Parece que el TSP ha sido discutido informalmente entre matemáticos en reuniones matemáticas durante muchos años«.
No obstante, parece haber un consenso general entre los estudiosos de este problema de optimización combinatoria, en el sentido de que la primera referencia del TSP aparece en Alemania, en el año 1.832, en un libro que lleva por título «El problema del viajero. Cómo debe hacer para tener éxito en sus negocios«. En el último capítulo del mismo se vislumbra la esencia del TSP.
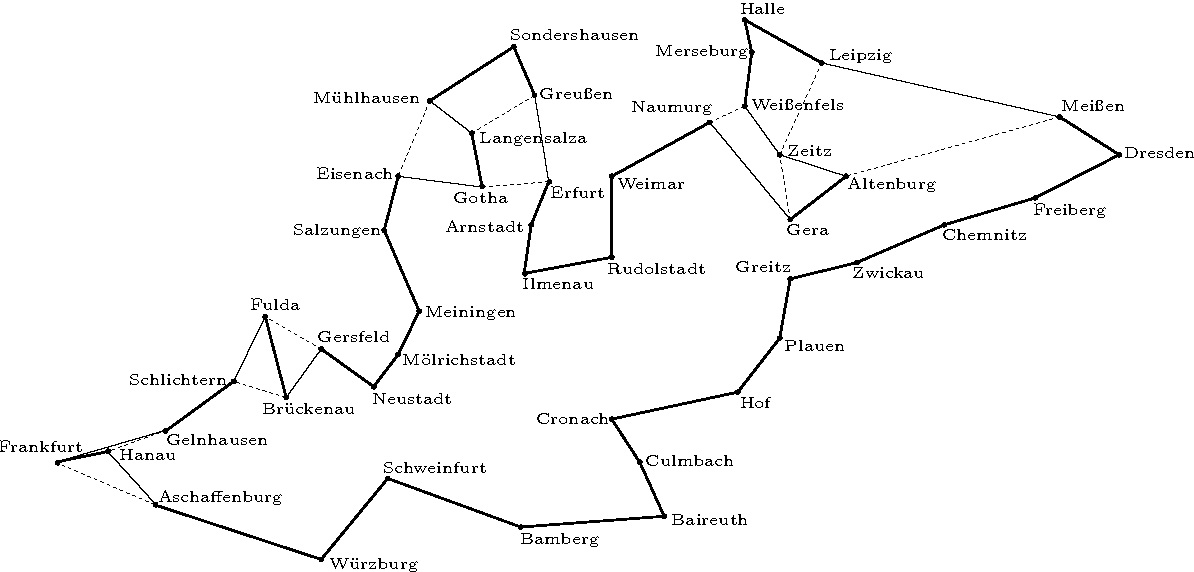
El TSP, en su versión más básica, fue propuesto por primera vez en las Universidades de Viena y Harvard en 1.930. Destaca el trabajo de Karl Menger, que presenta una formulación rigurosa del problema, propone un algoritmo para generar soluciones factibles y esboza algunos resultados relacionados con la complejidad del mismo.
A partir de la década de los 50 del siglo pasado, el TSP fue convirtiéndose en el objeto de estudio de los investigadores de la época, destacando el trabajo de Dantzig, Fulkerson y Johnson, quienes modelan el TSP como un problema de programación lineal entera y desarrollan un algoritmo de planos de corte para resolverlo. Tras aplicarlo a varios enunciados de problemas TSP, consiguen determinar la solución óptima en un problema de dimensión (número de localizaciones a visitar) 49.
Desde entonces, la dimensión de los problemas resueltos ha ido creciendo de forma considerable, y, hasta donde llega nuestro conocimiento, el problema resuelto de forma óptima corresponde con una dimensión de 85.900 localizaciones.
Complejidad del TSP
La complejidad del TSP es exponencial. Esto quiere decir que conforme aumente el número de localizaciones que han de formar parte de la ruta, el número de rutas factibles y, en consecuencia, el tiempo de computación preciso para resolver el problema crecen de forma exponencial.
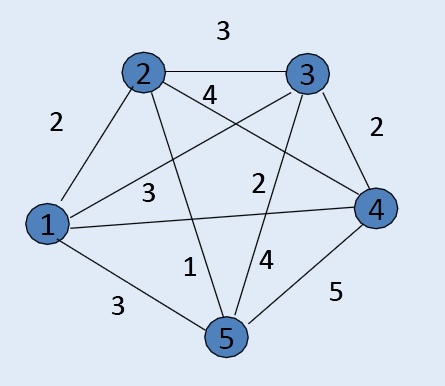
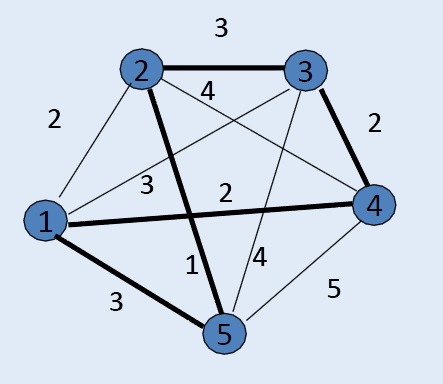
Daremos respuesta al enunciado del problema planteado anteriormente. Se presenta en forma de grafo, en el que los nodos representan las localizaciones a visitar y los arcos las rutas que los unen. Sobre estos arcos, figura el coste de transitarlos para desplazarse entre los nodos que une dicho arco.
En este problema, suponemos que el origen de las rutas es el nodo 1, y tras la finalización de las mismas, tras recorrer una única vez los nodos 2 a 5, el vehículo ha de retornar de nuevo al nodo 1.
No existe un procedimiento que proporcione la solución exacta del problema. Por ello, mientras la dimensión del problema lo permita, la mejor opción es resolverlo mediante el análisis de todas las soluciones posibles. Este método recibe varios nombres como el de fuerza bruta o exhaustivo.
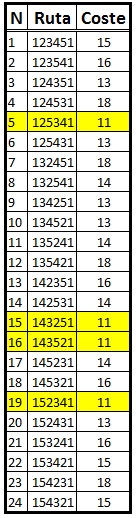
Este es el procedimiento seguido para determinar la solución de este problema. Cómo las rutas tienen su origen y fin en el nodo 1, existirán tantas rutas posibles como formas existan de ordenar los nodos restantes, es decir, los nodos 2, 3, 4 y 5. Por ello, existen 4!=24 rutas posibles.
El resultado de este análisis se muestras en la tabla de la derecha. En concreto, aparecen cada una de las 24 rutas (se puede comprobar como comienzan y finalizan en el nodo 1) y, para cada una de ellas, su coste asociado. Se puede comprobar como el coste mínimo que permite realizar la ruta con las restricciones del modelo es 11. Las rutas con este conste asociado son las número 5, 15, 16 y 17. En este caso, la solución del problema es un óptimo múltiple.
En este caso, hemos podido comprobar como la resolución de un problema de dimensión 4 (aunque son 5 nodos, sólo 4 de ellos son variables en las rutas, pues el nodo 1 es fijo al principio y final de la misma) ha exigido el análisis de 4! soluciones posibles. En general, se establece que un problema con n nodos (o de dimensión n) precisa del análisis de n! rutas.
Para ver el comportamiento de la función factorial, y analizar la complejidad del TSP, podemos estudiar la tabla siguiente:
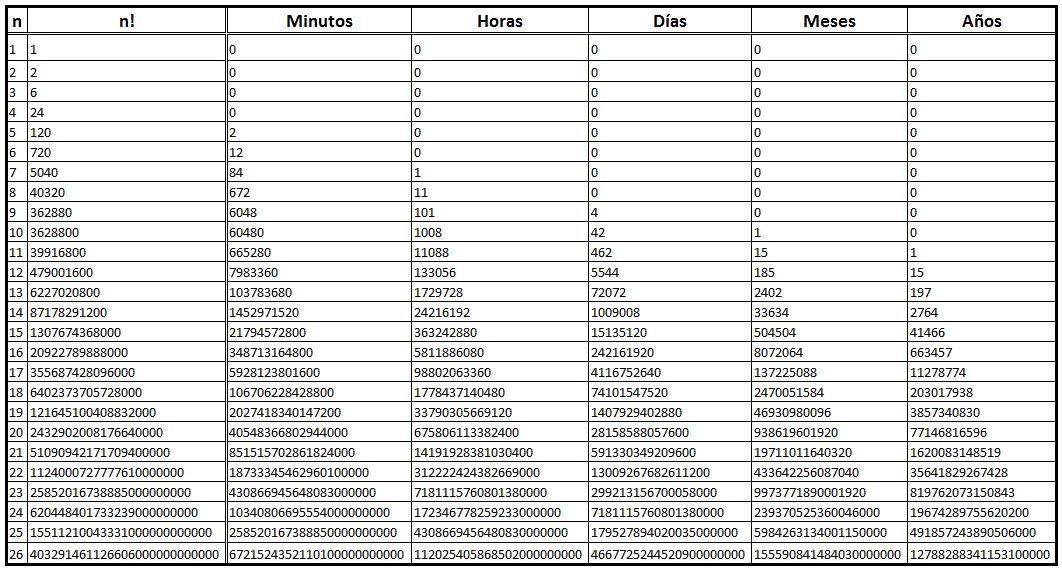
En la primera columna, con el encabezado N, aparece la dimensión del problema o número de nodos que componen la ruta. Se puede apreciar que esta tabla ofrece información para los valores n=1 a n=26. En la segunda columna, con el encabezado n! aparece el número de soluciones a analizar. Para confeccionar esta tabla se ha establecido la hipótesis de que la construcción de cada ruta y su análisis correspondiente (determinación del coste de la misma) precisan de 1 segundo de computación. Con esta hipótesis, los valores de esta segunda columna también indican los segundos de computación que cada problema precisaría. A continuación, y en las columnas siguientes, se transforma este tiempo en minutos, horas, días, meses y años.
Por llamar la atención en un sólo caso, podemos comprobar como un problema de dimensión 11 precisaría 1 año para su resolución bajo estas condiciones. Uno de 12 localizaciones precisaría de 15 años, mientras que uno de dimensión 13 necesitaría 197 años. Sin duda alguna, estas cifras permiten percibir ese crecimiento exponencial en la complejidad del problema.
Evidentemente, estos tiempos resultan inviables en la realidad. Por ello, se emplean otro conjunto de métodos de resolución, denominados heurísticos, que sacrifican la exactitud de la solución en aras de un tiempo de computación viable. Si bien estos métodos no garantizan la optimalidad de las soluciones, si se puede decir que, tras la correspondiente fase de configuración de los mismos, se obtienen soluciones de calidad más que aceptables.
Variantes del TSP
El modelo TSP presentado hasta este momento, corresponde a la versión básica de este problema. Existen otras versiones y extensiones del mismo que tienen en cuenta otros aspectos de la realidad o añaden restricciones adicionales a lo visto hasta este momento. Entre las versiones más empleadas, podemos citar:
- Versión asimétrica: Su peculiaridad radica en que dadas dos localizaciones, el coste para trasladarse de una a la otra no ha de coincidir necesariamente con el coste del traslado en el sentido inverso. Esta versión se emplea, por ejemplo, en modelos urbanos, en los que en ciertos momentos, los desplazamientos son muy distintos según su sentido. Es un ejemplo típico de horas puntas de entradas y salidas a las grandes ciudades en horas puntas.
- Versión no completa: Esta versión se caracteriza por el hecho de que desde cada localización no siempre es posible trasladarse a cualquier otra. Esta variante también es muy típica de entornos urbanos, donde existen múltiples restricciones a los desplazamientos de vehículos.
- Ventanas de tiempo: En esta versión, la visita a cada localización ha de realizarse en un periodo de tiempo determinado de antemano. Esta circunstancia impone un alto grado de secuencialidad a la rutas y, en consecuencia, puede quedar definida en gran medida por este tipo de restricciones temporales.
- Restricciones de precedencia: Esta versión del TSP aparece cuando se imponen restricciones en el sentido de que ciertas localizaciones han de ser visitadas antes que otras.
- Entregas y/o recogidas: La lógica primaria del TSP es visitar localizaciones con cierta finalidad. En la mayoría de los casos, las de entregar o recoger algún artículo. En otras ocasiones, pueden coincidir ambas situaciones (transporte público de viajeros). En todos estos casos aparecen un nuevos conjunto de restricciones que tienen que ver con la capacidad del vehículo. A partir de aquí, surge un nuevo modelo de rutas denominado Problema de rutas de vehículos.
Aunque no se trata de una variante, en este punto también resulta muy interesante destacar la introducción en el modelo de algunos aspectos medio ambientales. Así, por ejemplo, en la construcción de la función objetivo se tienen en cuenta no sólo los aspectos económicos, generalmente minimizar los costes, sino que que se introducen elementos que favorezcan las soluciones con menor emisión de gases o menor consumo de combustible. Igualmente, en los modelos se introducen junto a las localizaciones los diferentes puestos de recarga de vehículos eléctricos, de tal forma que la ruta óptima incluye los puntos de recarga entre las localizaciones a visitar. Estas nuevas características del modelo se pueden incluir en cualquiera de las variantes anteriores.
Aplicaciones del TSP
Sin duda alguna, la aplicación más evidente y conocida del TSP es la relacionada con la determinación de la ruta óptima que recorra un conjunto de localizaciones. Son muchos los ámbitos en los que puede emplearse este modelo: transporte público, servicios postal, recogida de residuos, tours turísticos, etc.
Existen otras aplicaciones quizá menos conocidas por ser más específicas, como son el taladrado de placas de circuitos impresos y la secuenciación de tareas, por ejemplo.


